Enhanced Lattice Basis Reduction Technique Revolutionizes Cryptography and Mathematics

The original version of this story appeared in Quanta Magazine.

Explore the groundbreaking improvements in lattice basis reduction, a key technique in cryptography and mathematics. Two researchers have developed a novel method, revolutionizing the field and opening doors to new possibilities in digital security.

Cryptography is essential to maintaining security in our increasingly digital lives. When you send a private message or make an online bill payment, algorithms created to protect your personal information are used. Naturally, some people want to uncover those secrets—so researchers work to test the strength of these systems to make sure they won’t crumble at the hands of a clever attacker.

Cryptography is essential to maintaining security in our increasingly digital lives. When you send a private message or make an online bill payment, algorithms created to protect your personal information are used. Naturally, some people want to uncover those secrets—so researchers work to test the strength of these systems to make sure they won’t crumble at the hands of a clever attacker.

Over the years, researchers have honed variants of LLL to make the approach more practical—but only up to a point. Now, a pair of cryptographers have built a new LLL-style algorithm with a significant boost in efficiency. The new technique, which won the Best Paper award at the 2023 International Cryptology Conference, widens the range of scenarios in which computer scientists and mathematicians can feasibly use LLL-like approaches.

Over the years, academics have improved variants of LLL to make the concept more practical—but only up to a point. Recently, two cryptographers have developed a new LLL-style method that has a notable increase in efficiency. The novel method expands on the variety of settings in which mathematicians and computer scientists can realistically apply LLL-like approaches; it was recognized with the Best Paper prize at the 2023 International Cryptology Conference.

In the realm of lattices, which are endless collections of points that are consistently spaced, LLL-type algorithms function. Imagine that you are tiling a floor to help you visualize this. You could cover it in square tiles, and the corners of those tiles would make up one lattice. Alternatively, you could choose a different tile shape—say, a long parallelogram—to create a different lattice.

The “basis” of a lattice can be used to characterize it. This is a set of vectors (essentially, lists of numbers) that you can combine in different ways to get every point in the lattice. Consider a lattice whose basis is made up of the vectors [1, 4] and [3, 2]. The lattice is just all the points you can reach by adding and subtracting copies of those vectors.

The lattice’s basis is not limited to that pair of vectors. There are an endless number of potential bases for each lattice having at least two dimensions. However, not every base is made equally. Researchers refer to bases that have vectors that are shorter and closer to a right angle with one another as “good” bases because they are generally easier to work with and more effective in solving specific computing issues. The two blue vectors in the graphic below serve as an illustration of this. Bases consisting of longer and less orthogonal vectors—like the red vectors—can be considered “bad.”

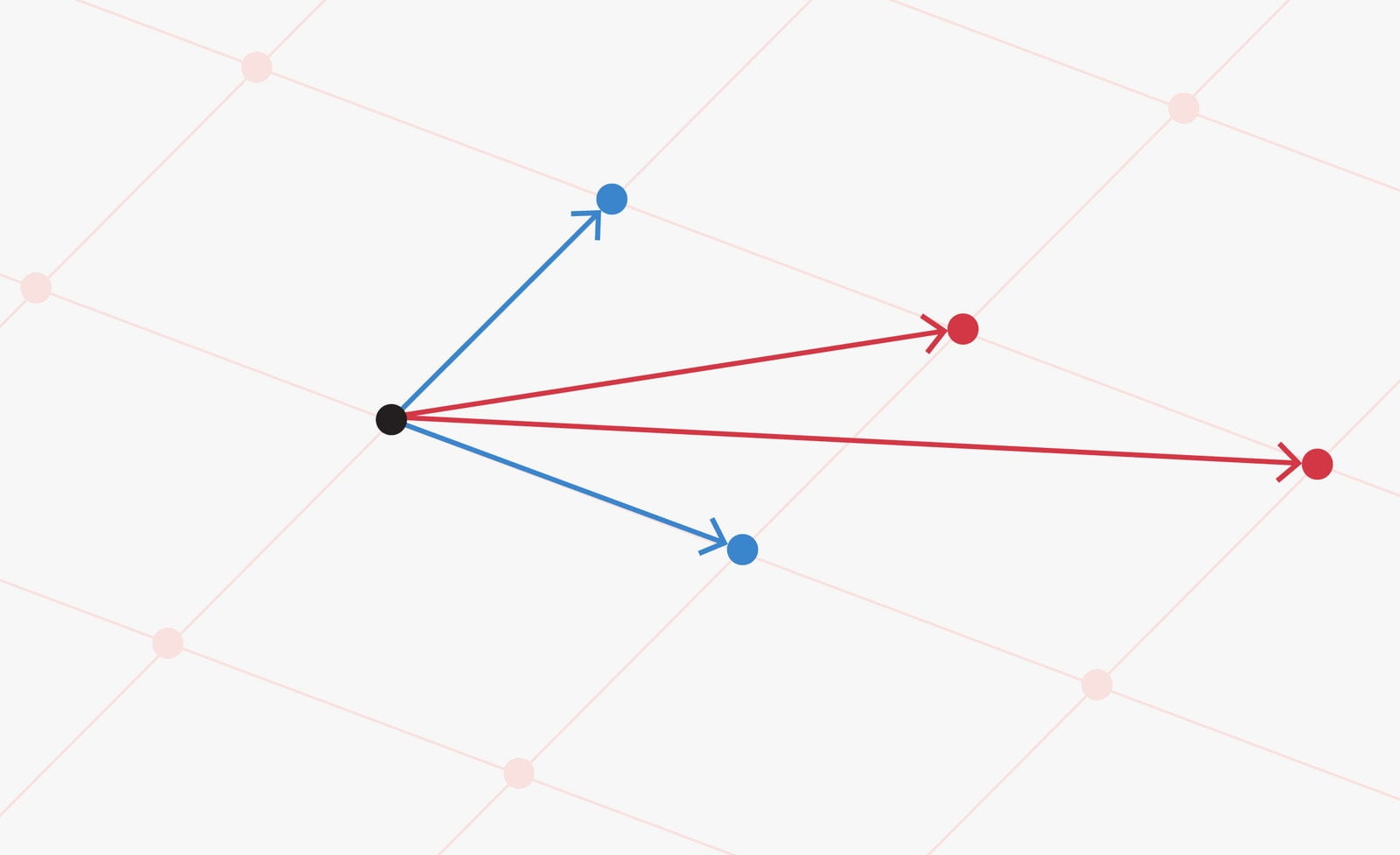
This is the task for LLL: Provide it (or its siblings) with a multidimensional lattice basis, and it will generate a superior one. Lattice basis reduction is the term for this procedure.

What connection does any of this have to cryptography? As it happens, there are situations when cracking a cryptographic system can be reframed as the process of locating a reasonably short vector within a lattice. Additionally, that vector may occasionally be extracted from the reduced basis produced by an algorithm in the LLL style. Using this tactic, scientists have been able to overthrow systems that superficially seem unrelated to lattices.

In a theoretical sense, the original LLL algorithm runs quickly: The time it takes to run doesn’t scale exponentially with the size of the input—that is, the dimension of the lattice and the size (in bits) of the numbers in the basis vectors. But it does increase as a polynomial function, and “if you actually want to do it, polynomial time is not always so feasible,” said Léo Ducas, a cryptographer at the national research institute CWI in the Netherlands.

This effectively indicates that too-large inputs cannot be handled by the original LLL algorithm. Keegan Ryan, a PhD candidate at the University of California, San Diego, stated that “mathematicians and cryptographers wanted the ability to do more.” Researchers worked to optimize LLL-style algorithms to accommodate bigger inputs, often achieving good performance. Still, some tasks have remained stubbornly out of reach.

The latest work, written by Ryan and his advisor Nadia Heninger, enhances the effectiveness of its LLL-style algorithm by combining many techniques. To start, the method divides the task into manageable portions by using a recursive structure. In addition, the algorithm finds a balance between speed and accuracy by meticulously controlling the precision of the numbers involved. Researchers can now lower the bases of thousands-dimensional lattices thanks to the latest work.

Previous research has taken a similar tack: Recursion and precision management are also combined in a 2021 publication to quickly process massive lattices; however, this method was limited to a subset of lattice types, not all of which are significant in cryptography. The new algorithm behaves well on a much broader range. “I’m really happy someone did it,” said Thomas Espitau, a cryptography researcher at the company PQShield and an author of the 2021 version. His team’s work offered a “proof of concept,” he said; the new result shows that “you can do very fast lattice reduction in a sound way.”

The novel method is already beginning to show benefits. Mathematician Aurel Page of the French national research institute Inria reported that he and his colleagues have applied an algorithmic adaptation to a few computational number theory challenges.

LLL-style algorithms may also be useful in the study of lattice-based cryptography systems that are intended to be safe in the event that quantum computing becomes a reality. Since taking down such systems requires finding shorter vectors than these algorithms can accomplish, they don’t represent a threat to them. But the best attacks researchers know of use an LLL-style algorithm as a “basic building block,” said Wessel van Woerden, a cryptographer at the University of Bordeaux. In practical experiments to study these attacks, that building block can slow everything down. Using the new tool, researchers may be able to expand the range of experiments they can run on the attack algorithms, offering a clearer picture of how they perform.

This article was originally published in Quanta Magazine, an editorially independent journal of the Simons Foundation. Its goal is to improve public understanding of science by reporting on trends and developments in mathematics, the physical and biological sciences, and research advances in these fields. Reprinted with permission.

Conclusion

The enhanced lattice basis reduction method developed by two researchers represents a significant breakthrough in cryptography and mathematics. With its potential to revolutionize digital security and computational mathematics, this advancement marks a pivotal moment in the field. As researchers continue to explore its implications, the future of cryptography and mathematical research looks promising and secure